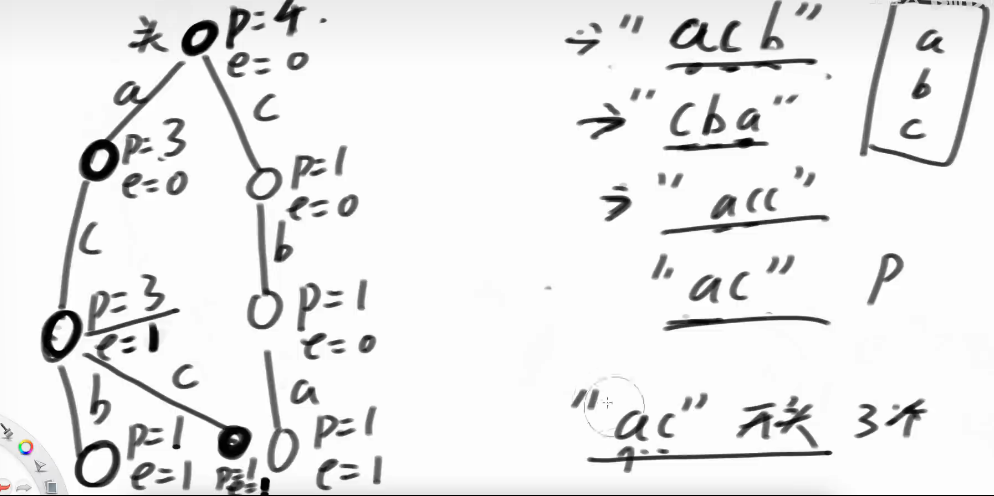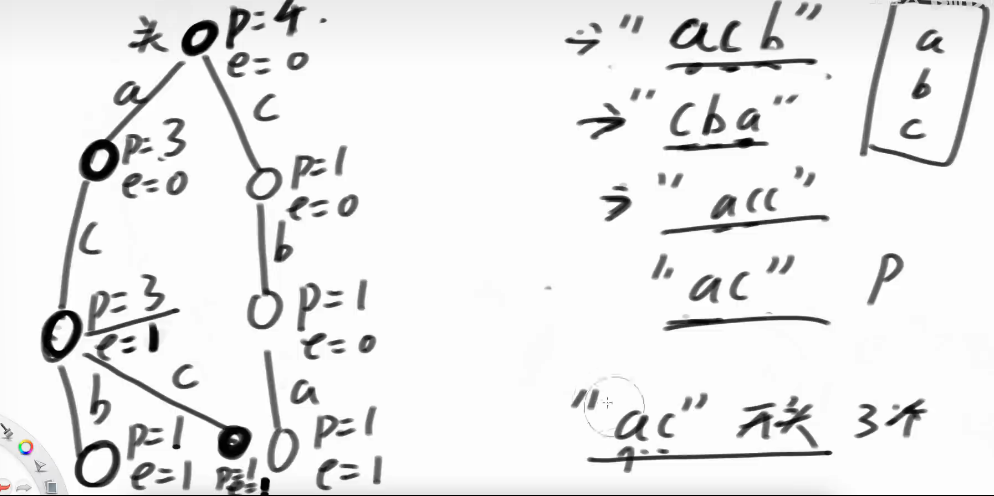前缀树基本知识
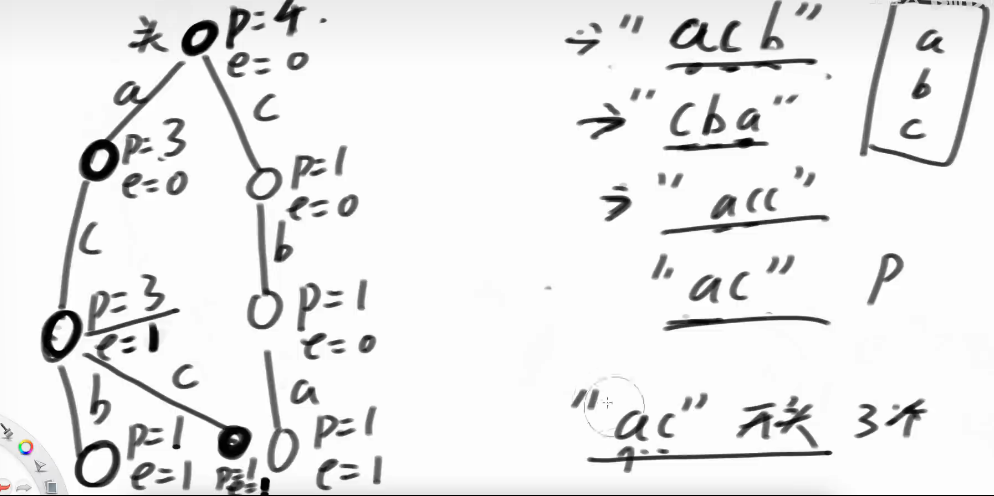
前缀树又叫字典树(trie),每个样本从头结点开始,根据前缀数据构建一个大树,没有路则新建结点,已经有路则复用结点,字符放在边上
使用场景: 需要根据前缀信息来查询
优点:根据前缀信息选择书上的分支,节省大量的时间
缺点:比较浪费空间,与总字符数量和字符种类(一个结点的路有很多条)有关
类描述实现前缀树
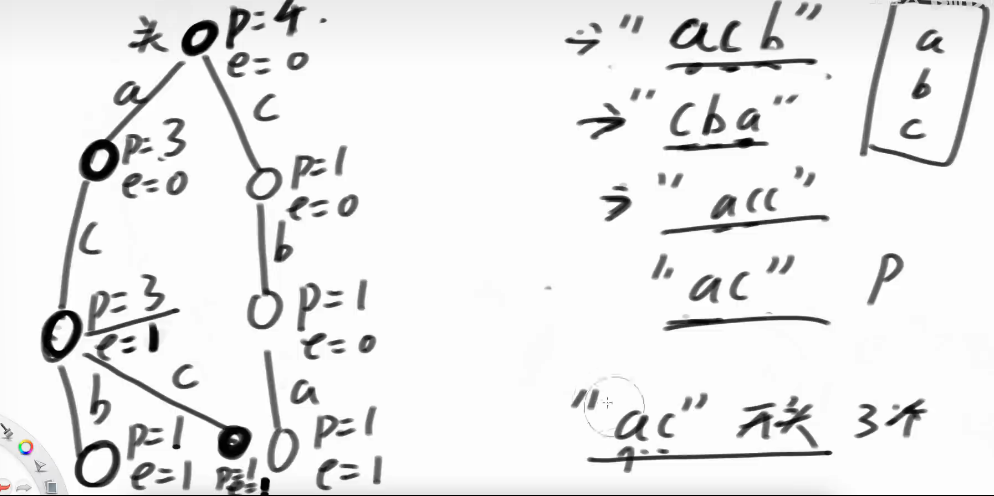
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
| class TrieNode{
public int pass;
public int end;
public TrieNode[] nexts;
public TrieNode(){
pass = 0;
end = 0;
nexts = new TrieNode[26];
}
}
private TrieNode root;
public Trie(){
root = new TrieNode()
}
public void insert(String word){
TrieNode node = root;
node.pass++;
for(int i = 0, path; i < word.length(); i++){
path = word.charAt(i) - 'a';
if(node.nexts[path] == null){
node.nexts[path] = new TrieNode;
}
node = node.nexts[path];
node.pass++;
}
node.end++;
}
public void erase(String word){
if(countWordEqualTo(word) > 0){
TrieNode node = root;
node.pass--;
for(int i = 0, path; i < word.length(); i++){
path = word.charAt(i) - 'i';
if(--node.nexts[path].pass == 0){
node.nexts[path] = null;
return;
}
node = node.nexts[path];
}
node.end--;
}
}
public int countWordEqualTo(String word){
TrieNode node = root;
for(int i = 0, path;i < word.length(); i++){
path = word.charAt(i) - 'a';
if(node.nexts[path] = null){
return 0;
}
node = node.nexts[path];
}
return node.end;
}
public int countWordStartingWith(String pre){
TrieNode node = root;
for(int i = 0, path; i <pre.length(); i++){
path = pre.charAt(i) - 'a';
if(node.nexts[path] == null){
return 0;
}
}
return node.pass;
}
|
也可以采用哈希表的方式来代替数组
静态数组实现前缀树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
| public static int MAXN = 150001;
public static int[][] tree = new int[MAXN][26];
public static int[] end = new int[MAXN];
public static int[] pass = new int[MAXN];
public static int cnt;
public static void build(){
cnt = 1;
}
public static void insert(String word){
int cur = 1;
pass[cur]++;
for (int i = 0, path; i < word.length(); i++){
path = word.charAt(i) - 'a';
if (tree[cur][path] == 0){
tree[cur][path] = ++cnt;
}
cur = tree[cur][path];
pass[cur]++;
}
end[cur]++;
}
public static int search(String word){
int cur = 1;
for (int i = 0, path; i < word.length(); i++){
path = word.charAt(i) - 'a';
if (tree[cur][path] == 0){
return 0;
}
cur = tree[cur][path];
}
return end[cur];
}
public static int prefixNumber(String pre){
int cur = 1;
for (int i = 0, path; i < pre.length(); i++){
path = pre.charAt(i) - 'a';
if(tree[cur][path] == 0){
return 0;
}''
cur = tree[cur][path];
}
return pass[cur];
}
public static void delete(String word){
if(search(word)> 0){
int cur = 1;
for (int i = 0, path; i < word.length(); i++){
path = word.charAt(i) - 'a';
if(--pass[tree[cur][path]] == 0){
tree[cur][path] = 0;
return;
}
cur = tree[cur][path];
}
end[cur]--;
}
}
public static void clear(){
for (int i = 1; i <= cnt; i++){
Arrays.fill(tree[i], 0);
end[i] = 0;
pass[i] = 0;
}
}
|
相关题目
接头密钥
牛牛和他的朋友们约定了一套接头密钥系统,用于确认彼此身份,密钥b的长度不超过必要a的长度,对于任意$0\leq i \leq length(b)$,有$b[i+1] - b[i] == a[i+1] - a[i]$,现在给定了m个密钥b的数组,以及n个密钥a的数组,请你返回一个长度为m的结果数组ans,表示每个密钥b都有多少一致的密钥数组a和数组b中的元素个数均不超过$10^5$,$1\leq m,n \leq 1000$