图的基本概念
图的定义
由顶点集$V$和边集$E$组成,记为$G=(V,E)$,$V(G)$表示图G中顶点的有限非空集合;$E(G)$表示图G中顶点之间的关系(边)集合,$|V|$表示顶点个数,$|G|$表示边的条数。
有向图:$E$为有向边的有限集合,$E_1=(<1,2>,<2,1>,<2,3>)$
无向图:$E$为无向边的有限集合,$E_2=((1,2),(1,3),(2,3))$
简单图:不存在重复边
完全图(简单完全图):无向图中任意两个顶点之间存在边,有向图中任意两个顶点之间都存在方向相反的两条弧
子图:两个图G=(V,E)和G’=(V’,E’),V’是V的子集,E’是E的子集,则称G’是G的组图。若有满足V(G’)=V(G)的子图G’,则称其为G的生成子图。
连通:无向图中,若从顶点v到顶点w有路径存在,则称v和w是连通的
连通图:若图G中任意两个顶点都是连通的,则称图G为连通图,否则称为非连通图。
连通分量:无向图中的极大连通子图称为连通分量
强连通图:在有向图中,若有一对顶点v和”,从v到w和从w到v之间都有路径,则称这两个顶点是强连通的。若图中任意一对顶点都是强连通的,则称此图为强连通图。
强连通分量:有向图中的极大强连通子图称为有向图的强连通分量。
生成树:生成树是包含图中全部顶点的一个极小连通子图,若图中顶点数n,则它的生成树含有n-1条边。
对生成树而言,若砍去它的一条边,则会变成非连通图,若加上一条边则会形成一个回路。
在非连通图中,连通分量的生成树构成了非连通图的生成森林。
度:顶点的度是指依附于顶点的边的条数,记为TD(v),无向图的全部顶点的度之和等于边数的两倍。
出度,入度:入度是以顶点v为终点的有向边的数目,记为ID(v);出度是以顶点v为起点的有向边数目,记为OD(v)
边的权和网:在一个图中,每条边都可以标上具有某种含义的数值,该数值称为该边的权值。这种边上带有权值的图称为带权图,也称网。
稀疏,稠密:边数很少的图称为稀疏图,反之称为稠密图。
一般当图 G满足|E|<|V|log|V|时,可以将 G视为稀疏图。
路径:指的是从一个顶点到另一个顶点的指顶点序列,路径上的边的数目称为路径长度,起点终点相同的路径称为回路或环。
若一个图有n个顶点,且有大于n-1条边,则此图一定有环。
简单路径/回路:在路径序列中,顶点不重复出现的路径称为简单路径。除第一个顶点和最后一个顶点外,其余顶点不重复出现的回路称为简单回路。
距离:从顶点u出发到顶点v的最短路径若存在,则此路径的长度称为从u到v的距离。,若不存在路径,则记该距离为无穷。
有向树:一个顶点的入度为0、其余顶点的入度均为1的有向图
图的存储及基本操作
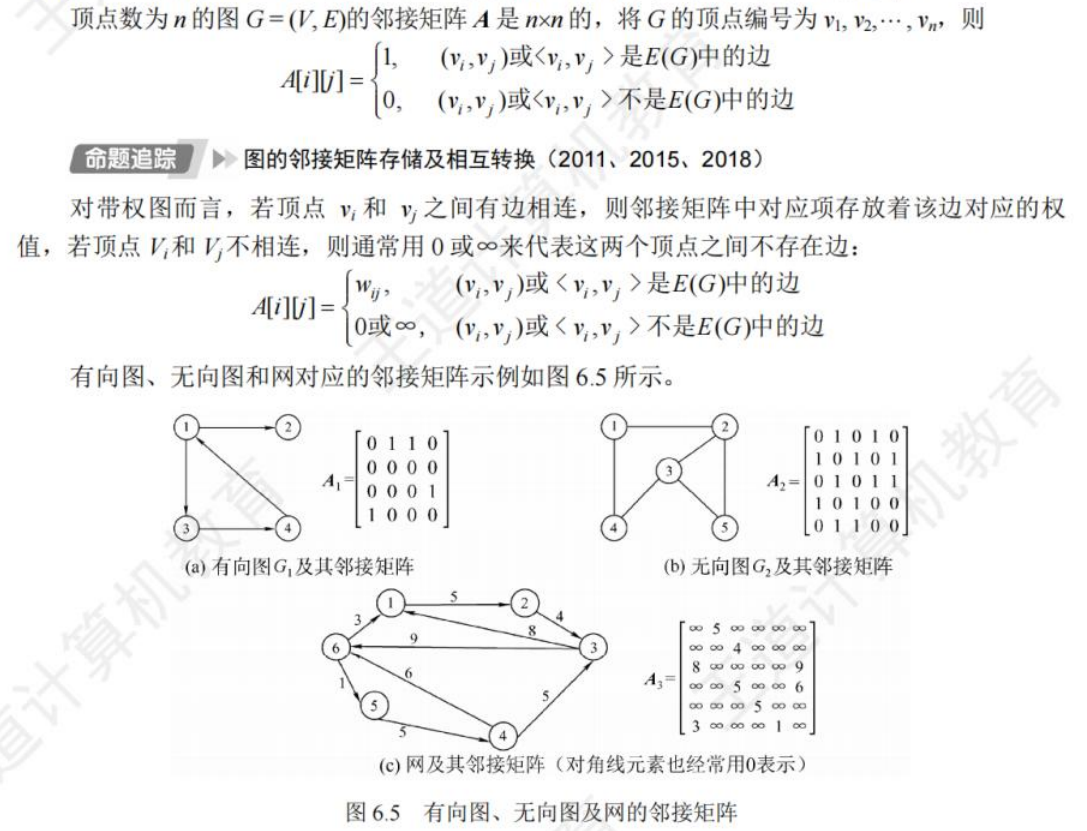
邻接矩阵法
用一个一维数组存储图中顶点的信息,用一个二维数组存储图中边的信息(即各顶点之间的邻接关系),存储顶点之间邻接关系的二维数组称为邻接矩阵。
邻接矩阵存储结构定义:
1
2
3
4
5
6
7
8
9
| #define MaxVertexNum 100
typedef char VertexType;
typedef int EdgeType;
typedef struct
{
VertexType vex[MaxVertexNum];
EdgeType edge[MaxVertexNum][MaxVertexNum];
int vexnum, arcnum;
} MGraph;
|
邻接矩阵特点:
- 无向图的邻接矩阵必是一个对称矩阵(并且唯一),因此可以直接存上三角或下三角矩阵。
- 对于无向图,邻接矩阵第i行/列的非零元素个数为顶点i的度TD(vi)
- 对于有向图,邻接矩阵第i行的非零元素个数为顶点i的出度OD(vi);邻接矩阵第i列的非零元素个数为顶点i的入度ID(vi)
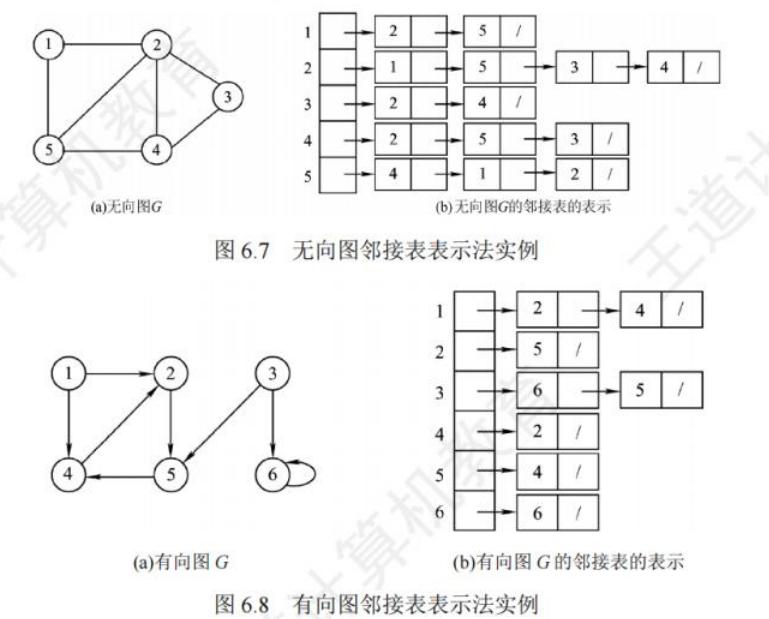
邻接表法
对图G的每个顶点$v_i$建立一个单链表,第i个单链表的结点表示依附于顶点$v_i$边(对于有向图则是以顶点$v_i$为尾的弧)),该单链表就称为顶点$v_i$的边表(对于有向图则称为出边表)。边表的头指针和顶点的数据信息采用顺序存储,称为顶点表

data存储顶点$v_i$的相关信息,边表头指针域指向第一条边的边表结点;边表的邻接点域存储与头结点顶点$v_i$邻接的顶点编号,指针域指向下一条边的边表结点。
邻接表存储结构定义:
一个数组存着该图的所有结点,每一个元素都为一个数组,存着以该结点为头的顶点表于边表结点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| #define MaxvertexNum 100
typedef char VertexType;
typedef struct ArcNode
{
int adjvex;
int info;
struct ArcNode *nextarc;
} ArcNode;
typedef struct VNode
{
int data;
ArcNode *firstarc;
} VNode,AdjList[MaxvertexNum];
typedef struct
{
AdjList vertices;
int vexnum, arcnum;
} ALGraph;
|
邻接表的特点:
- 若G为无向图,则所需的存储空间为$O(|V|+2|E|)$,每条边在邻接表中出现了两次;
- 若G为有向图,则所需的存储空间为$O(|V|+|E|)$;
十字链表
是有向图的一种链式存储结构
邻接多重表
图的基本操作
图的遍历
广度优先搜索
基本思想:
按数组顺序先遍历第一个元素,遍历其顶点表与边表,若没遍历过加入队列,若该元素完全遍历后,弹出队首元素遍历与其对应的顶点表与边表
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| #include <bits/stdc++.h>
using namespace std;
#define M 100
typedef char VertexType;
typedef struct ArcNode{
int adjvex;
int info;
struct ArcNode *nextarc;
}ArcNode;
typedef struct Vnode{
VertexType data;
ArcNode *firstarc;
}Vnode;
typedef struct{
Vnode Vertex[M];
int numV,numE;
}AdjList;
void bfs(AdjList G, int start)
{
bool visited[M] = {false};
queue<int> q;
visited[start] = true;
q.push(start);
while (!q.empty())
{
int v = q.front();
q.pop();
printf("%c ", G.Vertex[v].data);
ArcNode* p = G.Vertex[v].firstarc;
while (p != nullptr)
{
if (!visited[p->adjvex])
{
visited[p->adjvex] = true;
q.push(p->adjvex);
}
p = p->nextarc;
}
}
}
|
性能分析:
BFS求解单源最短路径问题:
在原有bfs的基础上,新增一个数组记录权值,当第一次遍历到或者权值小于原记录的权值时,将新权值与旧权值进行比较取min,新全值为当前顶点表+连到这一结点边的权值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
void bfs_shortest_path(AdjList G, int start)
{
vector<bool> visited(G.numV, false);
vector<int> distance(G.numV, INT_MAX);
queue<int> q;
visited[start] = true;
distance[start] = 0;
q.push(start);
while (!q.empty())
{
int v = q.front();
q.pop();
ArcNode* p = G.Vertex[v].firstarc;
while (p != nullptr)
{
if (!visited[p->adjvex] || distance[v] + p->info < distance[p->adjvex])
{
visited[p->adjvex] = true;
distance[p->adjvex] = min(distance[p->adjvex], distance[v] + p->info);
q.push(p->adjvex);
}
p = p->nextarc;
}
}
cout << "从起始顶点 " << G.Vertex[start].data << " 到各顶点的最短路径长度:" << endl;
for (int i = 0; i < G.numV; i++)
{
cout << "到顶点 " << G.Vertex[i].data << " 的最短路径长度为:" << distance[i] << endl;
}
}
|
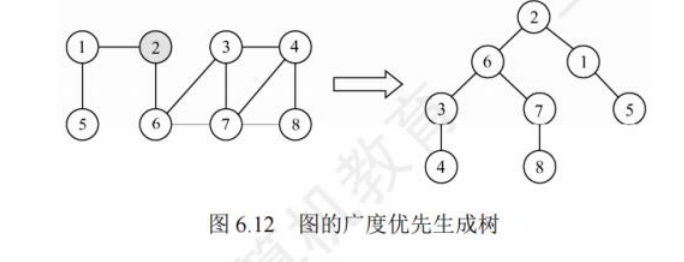
广度优先生成树:
通过广度优先遍历,我们可以得到一棵遍历树,称为广度优先生成树。
基于邻接表存储生成的树是不唯一的
深度优先搜索
类似于树的先序遍历,尽可能的深。
基本思想:
从第一个头结点开始,寻找其边表结点,在找到以该边表结点为头结点的邻接表,依次向下递归,直到遍历完全部元素。
代码实现:
递归实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| #include <bits/stdc++.h>
using namespace std;
#define M 100
typedef char VertexType;
typedef struct ArcNode{
int adjvex;
int info;
struct ArcNode *nextarc;
}ArcNode;
typedef struct Vnode{
VertexType data;
ArcNode *firstarc;
}Vnode;
typedef struct{
Vnode Vertex[M];
int numV,numE;
}AdjList;
void dfs_recursive(const AdjList &G, int v, vector<bool> &visited)
{
visited[v] = true;
cout << G.Vertex[v].data << " ";
ArcNode* p = G.Vertex[v].firstarc;
while (p != nullptr)
{
if (!visited[p->adjvex])
{
dfs_recursive(G, p->adjvex, visited);
}
p = p->nextarc;
}
}
void dfs(const AdjList &G, int start)
{
vector<bool> visited(G.numV, false);
dfs_recursive(G, start, visited);
}
|
非递归实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
void dfs(const AdjList &G, int start)
{
vector<bool> visited(G.numV, false);
stack<int> s;
s.push(start);
while (!s.empty())
{
int v = s.top();
s.pop();
if (!visited[v])
{
visited[v] = true;
cout << G.Vertex[v].data << " ";
ArcNode* p = G.Vertex[v].firstarc;
while (p != nullptr)
{
if (!visited[p->adjvex])
{
s.push(p->adjvex);
}
p = p->nextarc;
}
}
}
}
|
其空间复杂度为O(|V|),采用邻接矩阵存储时,时间复杂度为O(|V|²),采用邻接表存储时,时间复杂度为O(|V|+|E|)
深度优先生成树:
对连通图调用DFS才能产生深度优先生成树,否则产生的时深度优先森林。
基于邻接表存储生成的树是不唯一的
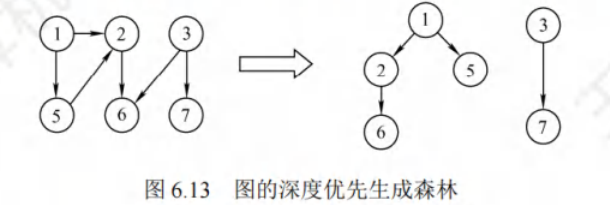
图的遍历与连通性

图的应用
最小生成树
生成树:包含所有的顶点,只含尽可能少的边,生成树少一条边为非连通图,多一条边形成回路。
对于一个带权的无向连通图,权值和最小的生成树位最小生成树
性质:
- 若存在权值相同的边,则最小生成树可能不唯一,权值都不相同 ,则最小生成树是唯一的
- 当最小生成树不唯一时,其对应的边的权值之和是唯一的
- 最小生成树的变数为顶点数-1
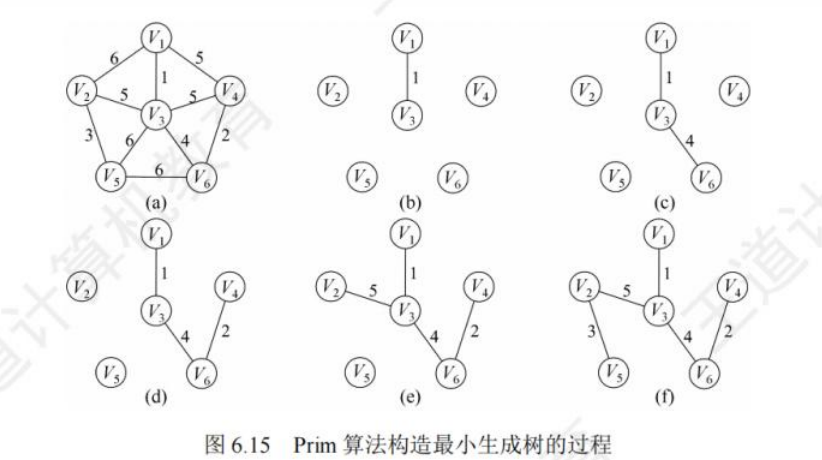
prim算法(不常用,常用k):
算法过程:
- 解锁点的集合为set,解锁边的集合为heap(小根堆),初始都为空
- 从给定点开始,开始点加入到set,开始点的所有边加入到heap
- 从heap中弹出权值最小的边e,查看该边的另一结点x
- 若x已在set内,舍弃e,重复步骤三
- 若x不在set内,把x加入set,x的所有边加入heap重复步骤三
- 当heap为空停止,得到最小生成树
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
| #include <bits/stdc++.h>
using namespace std;
#define M 100
typedef char VertexType;
typedef struct ArcNode{
int adjvex;
int info;
struct ArcNode *nextarc;
}ArcNode;
typedef struct Vnode{
VertexType data;
ArcNode *firstarc;
}Vnode;
typedef struct{
Vnode Vertex[M];
int numV,numE;
}AdjList;
void prim(const AdjList &G, int start)
{
vector<int> lowcost(G.numV, INT_MAX);
vector<int> mst(G.numV, -1);
vector<bool> inMST(G.numV, false);
lowcost[start] = 0;
for (int i = 0; i < G.numV; ++i)
{
int u = -1;
int minCost = INT_MAX;
for (int j = 0; j < G.numV; ++j)
{
if (!inMST[j] && lowcost[j] < minCost)
{
u = j;
minCost = lowcost[j];
}
}
if (u == -1)
break;
inMST[u] = true;
ArcNode* p = G.Vertex[u].firstarc;
while (p != nullptr)
{
int v = p->adjvex;
if (!inMST[v] && p->info < lowcost[v])
{
lowcost[v] = p->info;
mst[v] = u;
}
p = p->nextarc;
}
}
cout << "最小生成树的边:" << endl;
for (int i = 0; i < G.numV; ++i)
{
if (mst[i] != -1)
{
cout << G.Vertex[mst[i]].data << " - " << G.Vertex[i].data << " 权值:" << lowcost[i] << endl;
}
}
}
|
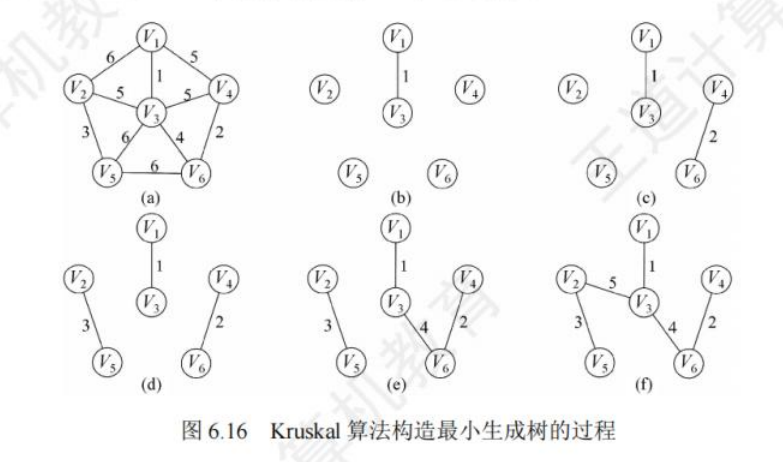
Kruskal算法:
算法过程:
- 把所有边根据权值大小进行排序,从权值小的边开始考虑
- 如果连接当前的边不会形成环,就选当前的边。否则就不选择
- 当边数为
n-1时,便可得到最小生成树。
代码实现:
并查集实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
| #include <bits/stdc++.h>
using namespace std;
#define M 100
typedef char VertexType;
typedef struct ArcNode{
int adjvex;
int info;
struct ArcNode *nextarc;
}ArcNode;
typedef struct Vnode{
VertexType data;
ArcNode *firstarc;
}Vnode;
typedef struct{
Vnode Vertex[M];
int numV,numE;
}AdjList;
class UnionFind {
public:
UnionFind(int n) : parent(n), rank(n, 0) {
for (int i = 0; i < n; ++i) {
parent[i] = i;
}
}
int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
void unite(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) {
if (rank[rootX] > rank[rootY]) {
parent[rootY] = rootX;
} else if (rank[rootX] < rank[rootY]) {
parent[rootX] = rootY;
} else {
parent[rootY] = rootX;
++rank[rootX];
}
}
}
private:
vector<int> parent;
vector<int> rank;
};
void kruskal(const AdjList &G, const vector<Edge>& edges)
{
sort(edges.begin(), edges.end());
UnionFind uf(G.numV);
vector<Edge> mst;
int mst_weight = 0;
for (const auto& edge : edges)
{
if (uf.find(edge.u) != uf.find(edge.v))
{
uf.unite(edge.u, edge.v);
mst.push_back(edge);
mst_weight += edge.weight;
}
}
cout << "最小生成树的边:" << endl;
for (const auto& edge : mst)
{
cout << G.Vertex[edge.u].data << " - " << G.Vertex[edge.v].data << " 权值:" << edge.weight << endl;
}
cout << "最小生成树的总权值:" << mst_weight << endl;
}
|
最短路径
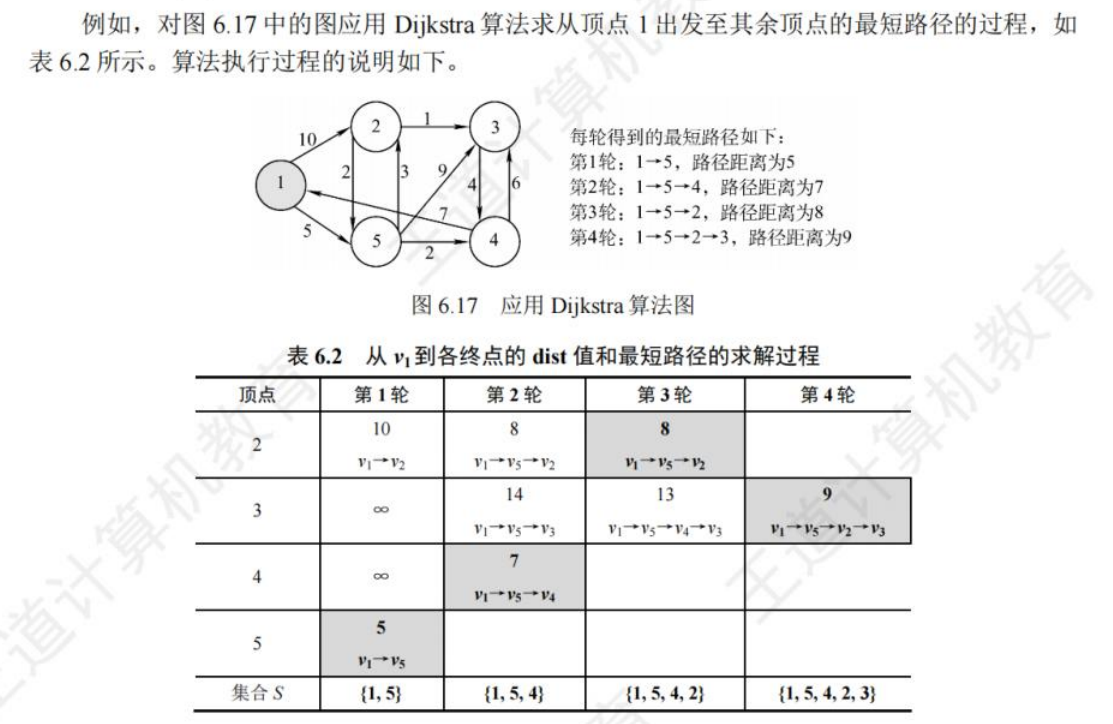
Dijkstra算法:
给定一个源点,求解 从源点到每个点的最短路径长度的单源最短路径算法。(边权值不为负数)
算法思想:
distance[i]表示从源点到i点的最短距离,visited[i]表示i结点是否从小根堆弹出过;- 准备小根堆,存放(x点,源点到x距离)
- 令
distance[源点]=0,(源点,0)进入小根堆
- 从小根堆弹出(u点,源点到u的距离)
- 若
visited[u]==true,不做任何处理,重复步骤4
- 若
visited[u]==false,令visited[u]==true,然后观察u的每一条边,设某边去往v,权值 为w
- 若
distance[u]+w<distance[v],令distance[v]=distance[u]+w,把(v,distance[u]+w)加入小根堆
- 处理完u的每一条 边后 ,重复步骤4
- 当小根堆为空后结束,
distance记录了源点到每一个结点 的最短距离
代码实现:
Floyd算法:
distance[i][j]存放i点到j点的最短距离- 通过枚举每个跳板三重for循环寻找
i到j的的最短距离,跳板要优先枚举
代码实现:
1
2
3
4
5
6
7
8
9
| for(int bridge = 0; bridge < n;bridge++){
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
if(distance[i][bridge] != Max_VALUE && distance[briidge][j] != MAX_VALUE && distance[i][j] > distance[i][bridge] + distance[bridge][j]){
distance[i][j] = distance[i][bridge] + distance[bridge][j];
}
}
}
}
|
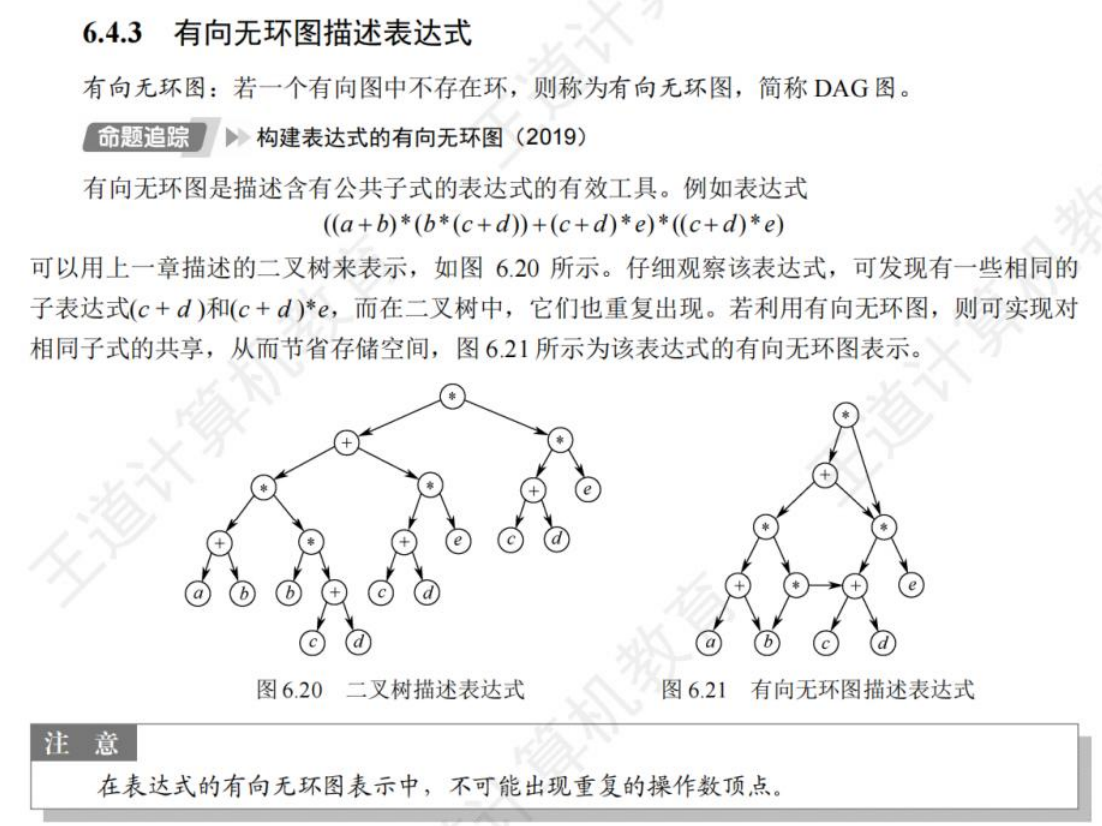
有向无环图描述表达式
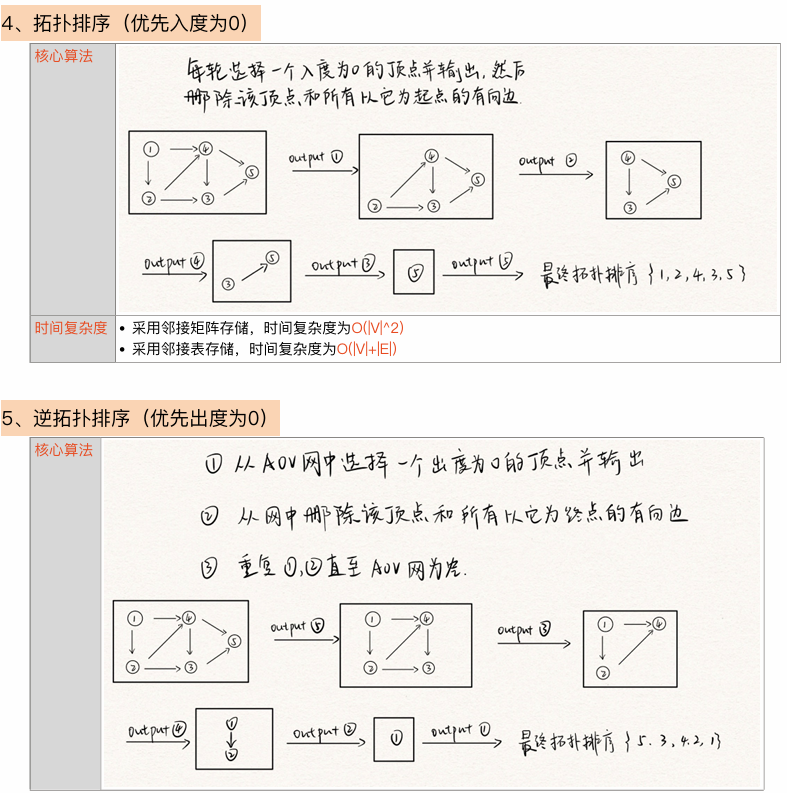
拓扑排序(AOV网)
步骤:
- 从AOV网中选择一个没有前驱(入度为0)的顶点并输出
- 从网中删除该顶点和所有以它为起点的有向边
- 重复1和2直到当前的AOV网为空或当前网中不存在无前驱的顶点位置,后一种情况说明有向图的中必然存在环。

关键路径(AOE网)
在带权有向图中,以顶点表示时间,以有向边表示活动,以边上的权值表示完成该活动的开销(如完成活动所需的时间),称为用边表示活动的网络,简称AOE网
性质:
- 只要在某顶点所代表的事件发生后,从该顶点出发的各有向边所代表的活动才能开始;
- 只要在进入某顶点的各有向边所代表的活动都已结束时,该顶点所代表的事件才能发生
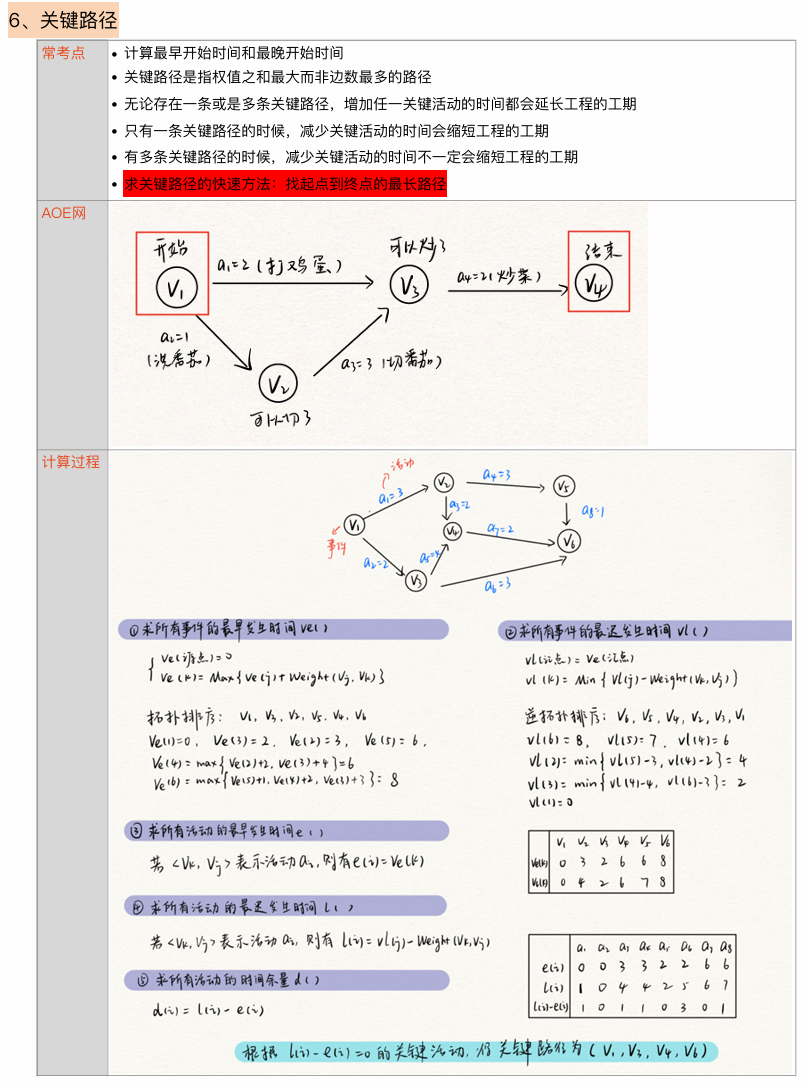
在AOE网中仅有一个入读为0的顶点,为开始顶点(源点),也仅有一个出度为0的顶点,为结束顶点(汇点)。从源点到汇点的所有路径中,具有最大路径长度的路径称为关键路径,关键路径上的活动称为关键活动。
求解过程:
- 从源点出发,令$v_e(源点)=0$,按拓扑有序求其余顶点的最早发生事件$v_e()$。
- 从汇点出发,令$v_l(汇点)=v_e(汇点)$,按逆拓扑有序求其余顶点的最迟发生时间$v_l()$。
- 根据各顶点的$v_e()$值求所有弧的最早开始时间$e()$。
- 根据各顶点的$v_l()$值求所有弧的最迟开始时间$l()$。
- 求AOE网中所有活动的差额$d()$,找出所有$d()=0$的活动过程关键路径