数据的表示和运算
数制与编码
| 原码 | 补码 | |
|---|---|---|
| 正数 | 本身 | 本身 |
| 负数 | 正数原码修改符号位 | 负数原码除符号位取反 + 1 |
| 8 | 00000000 00000000 00000000 00001000 | 00000000 00000000 00000000 00001000 |
| -8 | 10000000 00000000 00000000 00001000 | 11111111 11111111 11111111 11111000 |
得到一个相反数,除全部取反再+1
进位计数制及其相互转换
进制类型:
二进制(B):逢二进一
八进制(O):逢八进一
十进制(D)
十六进制(H):逢十六进一
进制转换:
二转八:三位二进制为一位八进制
二转十六:四维二进制转一位十六进制
八转十六:八转二再二转十六
十进制转二进制:
整数部分:除2所余下来的数可看作原数减去一个$2^n$所剩下来的数,自然便放在低位。

小数部分:每个数位的权值为$2^{-n}$形式,以0.5,0.25,0.125递减,一开始小数部分乘2如果大于1,那么意味着原小数大于0.5,再对剩余的小数部分乘2,实际就是对原来该部分乘4,并以此类推

定点数的编码表示
带正负号的数称为真值,即为实际值,将符号与数值一起编码后的数称为机器数。
机器数表示(补码整数表示整数,原码小数表示浮点数的尾数部分,移码表示浮点数的阶码部分):
- 定点表示,表示定点小数/整数,小数点位置确定
- 浮点表示:表示浮点小数,小数点位置不固定
原码
机器数最高位表示数的符号,其余各位表示数的绝对值
补码
正数的补码和原码相同,负数的补码为除符号位以外取反+1
实现了加减码的统一,原码的正负数只有符号位的不同,但这不符合加减法的规则,比方说
10000001正常来说进行加一操作后应当为0,但通过二进制的加法后却是-2,与我们所认知的加法所矛盾,,因此采用补码。在补码中
-1表示为11111111,进行加一操作为00000000,符合加减法的逻辑,$2^7-1=原码+补码-1$
反码
各位相反,不修改符号位
移码
实际值X上加上一个常数(偏置值),偏置值通常取$2^{n-1}$
阶码:浮点数整数部分中最大2的整数倍所对应的指数,具体见浮点数部分,同理于十进制的科学计数法。
相当于X在数轴上像正方向平移了若干单位,其中机器字长为$n$,未到八位把八位(此时偏置值为$2^7$)
阶码在浮点数的整数部分为0时,可能为负数
整数表示
在运算过程中采用补码进行运算,范围为$-2^{n-1}\sim 2^{n-1}-1$
运算方法和运算电路
基本运算部件
带标志加法器
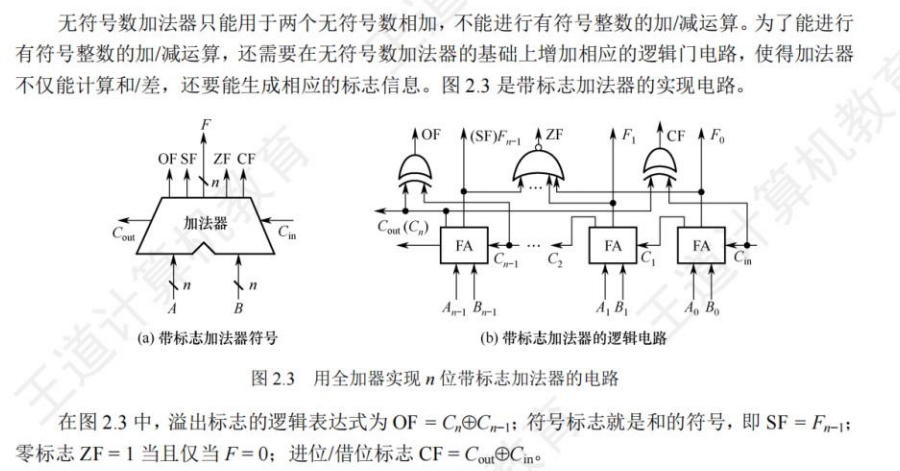
算术逻辑单元
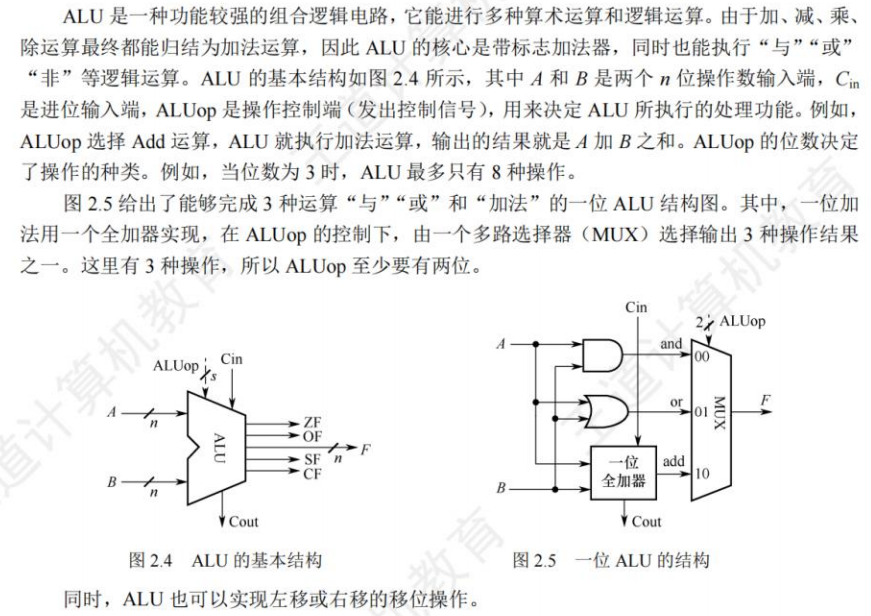
定点数的移位运算
右往左移,低位补零;左往右移,高位补零
逻辑移位
将操作数视为无符号整数,右往左移,低位补零;左往右移,高位补零.
算术移位
需要考虑符号位的问题,
定点数的加减运算
- 按二进制运算规则运算,逢二进一。
- 若做加法,两个数的补码直接相加;若做减法,则将被减数与减数的负数补码相加。
- 符号位与数值位一起参与运算,加、减运算结果的符号位也在运算中直接得出。
- 最终运算结果的高位丢弃,保留n+1位,运算结果亦为补码。
溢出处理
定点数的乘除运算
定点数乘法
乘法时,数值是直接使用绝对值来进行计算的,因此可以直接原码相乘,符号位异或运算,采用双符号位。
以下位小数部分的乘法:

$$
P_n=X×Y
$$
整数部分相乘可类比,为左移$0,1,…,n-1$位,两个定点小数相乘,可以将两个小数左移转为整数,再进行整数相乘,将计算的结果再右移来进行补偿。
乘法运算电路

定点数除法
计算机内部的除法运算与手算除法一样,通过被除数(中间余数)减除数来得到每一位商,够减上商 1,不够减上商0。原码除法运算也要将符号位和数值位分开处理,商的符号位是两个数的符号位的“异或”结果,商的数值位是两个数的绝对值之商。

除法运算电路
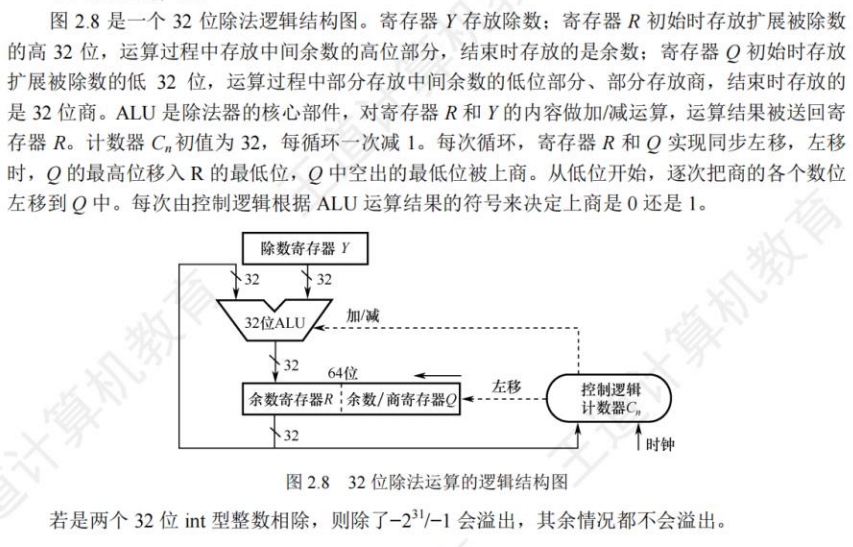
浮点数的表示与运算
浮点数的表示
浮点数结构(IEEE 754 单精度浮点数)
可表示的小数的小数部分的位数不固定。
设我们用浮点数表示8.0,它的二进制表示为1000.0,可以表示为$8.0=1.0×2^3$,尾数为1.0,阶码/指数为3,基数通常为2。
设我们用浮点数表示0.875,它的二进制表示为0.111,可以表示为$0.875=1.11×2^{-1}$,尾数为1.11,阶码/指数为-1但实际存储的是移码-1+127=126,二进制表示为01111110
在IEEE 754 单精度浮点数中,尾数会去掉整数部分和小数点,从第二位开始,不足二十三位自动填充至二十三位。
浮点数的表示范围:

- 运算结果大于最大正数时称为正上溢,小于最小负数时称为负上溢,产生上溢必须进行溢出处理
- 运算结果大于最大负数小于0为负下溢,,小于最小正数大于0为正下溢。,夏一时,浮点数趋于零,计算机将其当作机器0处理
下溢因为指数即移码的精度不够(特指整数部分位0的情况,因为此时移码为负数。小数越小,负数越大),当小数很小的时候就无法进行表示,因此会把小数当为0
上溢则是整数部分的绝对值过大,超出了移码所能表示的范围
区别于溢出,尾数精度不足则是指整数部分不为0,单纯浮点的数位超出了尾数所能记录的范围。
浮点数规格化
指通过调整一个非规格化的浮点数的尾数和阶码的大小,使非零浮点数在尾数的最高数位上保证是一个有效值,其实就是浮点数转二进制后的移位操作。
左规:尾数最高位为零,小数点前的数都为0
右规:小数点前不止一位有效位
IEEE 754标准
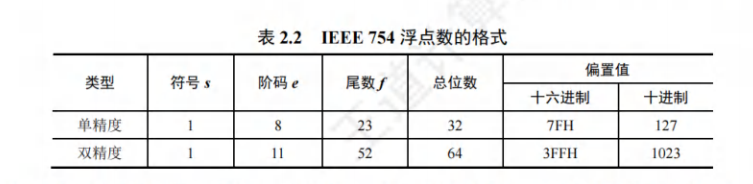
尾数用原码表示,规格化后尾数第一位必定为1,因此隐藏该位吗,称为隐藏位,小数点在隐藏位后,在该标准下,偏置值取得是$2^{n-1}-1$而非$2^{n-1}$
浮点数的加减运算
- 对阶:通过左右移调整两数的阶码一致,由于采用科学计数法,因此通常是向阶码大的一方看齐。
- 尾数加减:注意是否存在隐藏位,尾数加减时可以看作为绝对值相加减,符号取决于绝对值大的数。
为什么这里用的是原码,因为这里的符号位和尾码是分开存储,因此可以直接不带符号位进行计算,所以可以直接使用原码相加减
- 尾数规格化:同浮点数规格化,使小数点前只有一位有效位
- 舍入:当右移时,可能出现超出范围的情况,需要进行舍入
- 溢出判断:两个浮点数相加减可超出了可表示的范围,超过最大值为指数上溢,小于最小值为指数下溢,通常把结果按机器零处理。
数据的大小端和对齐存储
大小端存储
使用最低有效字节LSB和最高有效字节MSB分别表示数的低位。
大端方式:先存储高位字节,后存储低位字节,字中的字节顺序和原序列的相同,按MSB到LSB的顺序存储数据。
小端方式:先存储低位字节,后存储高位字节。字中的字节顺序和原序列的相反,按LSB到MSB的顺序存储数据。
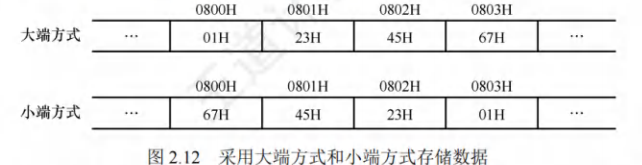
边界对齐存储
要求其存储的地址是自身大小的整数倍,半字地址一定是2的整数倍,字地址一定是4的整数倍,虽然浪费了一些存储空间,但提高了存储数据的速度。