随机事件与概率(对立一定互斥)
知识框架
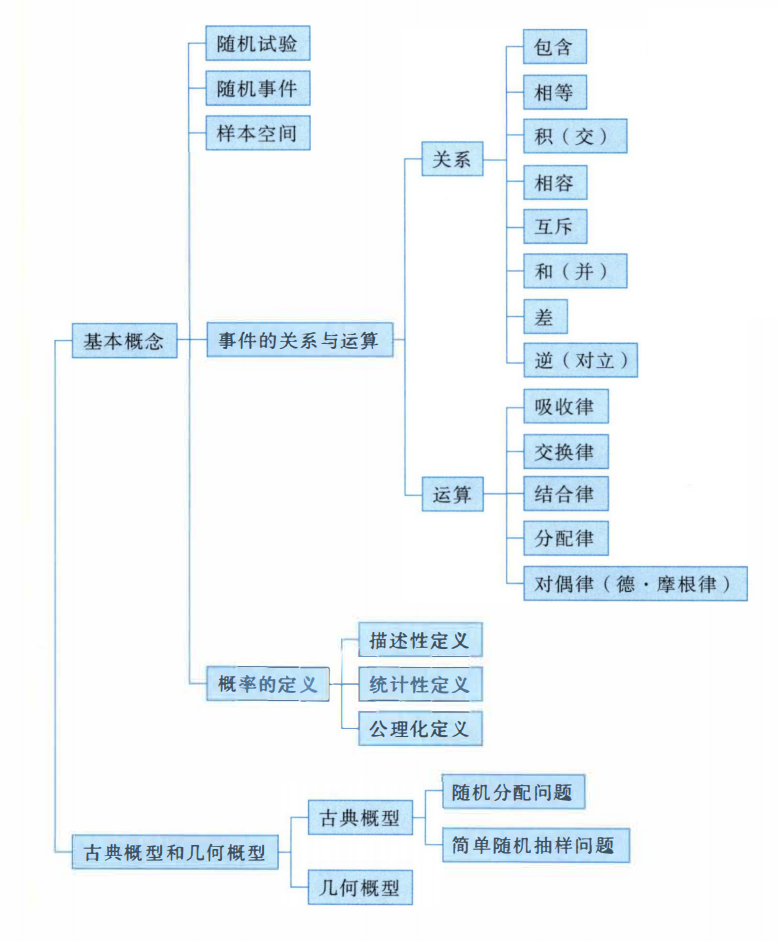
基本概念
随机试验
随机试验条件:
- 试验可以在相同的条件下重复进行;
- 试验所有可能结果明确可知,且不止一个;
- 每一次试验会出现哪一个结果,事先并不能确定
随机试验简称试验,用字母 $E_i$ 表示
随机事件
在一次试验中可能出现,也可能不出现的结果称为 随机事件,简称 事件,并用大写字母 A, B, C 等表示。将每次试验中一定发生的事件称为 必然事件,记为 $\Omega$。每次试验中一定不发生的事件称为 不可能事件,记为 ∅。
样本空间
随机试验的每一个可能结果称为样本点,记为 $\omega$。样本点的全体组成的集合称为样本空间(或基本事件空间),记为$\Omega $,即$\Omega = {\omega}$,由一个样本点构成的事件称为基本事件.随机事件A总是由若千个基本事件组成,即A是$\Omega$的子集。
事件关系与运算
关系:对立一定互斥
- 包含
- 相等
- 和(并):至少有一个发生
- 积(相交):两个同时发生
- 相容:$AB≠ ∅$
- 互斥(互不相容):$AB= ∅$
- 对立:$AB= ∅,A∪B=\Omega$
- 差:$A-B$ A发生而B不发生
- 逆:$B=\bar{A}$
完备事件组: 如果$\bigcup_{i=1}^{n} A_i = \Omega$(或$\bigcup_{i=1}^{\infty} A_i = \Omega$)且$A_i \cap A_j = ∅set(\text{对一切 } i \neq j;i, j = 1, 2, \dots, n(\dots)),$称有限(或可列)事件 ( A_1, A_2, \dots, A_n (\dots) ) 构成一个完备事件组。
运算:
吸收律:
若 A ⊆ B, 则 A ∪ B = B, A ∩ B = A。交换律:
A ∪ B = B ∪ A, A ∩ B = B ∩ A。结合律:
(A ∪ B) ∪ C = A ∪ (B ∪ C), (A ∩ B) ∩ C = A ∩ (B ∩ C)。分配律:
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C),
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C),
A ∩ (B - C) = (A ∩ B) - (A ∩ C)。对偶律 (德·摩根律):
A ∪ B = A̅ ∩ B̅,
A ∩ B = A̅ ∪ B̅。$A\bar{B}=A-AB=A-B$
注:
- 事件运算顺序约定为先进行逆运算,然后进行交运算,最后进行并或差运算。
- 事件的关系、运算与集合的关系、运算相当,且具有相同的运算法则,所以我们可以对比着理解记忆,并要学会用集合关系去考虑事件关系。
概率的定义
描述性定义:
通常将随机事件A发生的可能性大小的度量(非负值)称为事件A发生的概率,记为P(A)
统计性定义:
在相同条件下做重复试验,事件A出现的次数k和总的试验次数n之比$\frac{k}{n}$称为事件A在这n次试验中出现的频率.当试验次数n充分大时,频率将“稳定”于某常数p.”越大,频率偏离这个常数p的可能性越小.这个常数p就称为事件A的概率。
公理化定义:
设随机试验的样本空间为 $\Omega$,如果对每一个事件 $A$ 都有一个确定的实数 (P(A)),且事件函数 $P(\cdot)$ 满足:
非负性:$P(A) \geq 0$;
规范性:$P(\Omega) = 1$;
可列可加性:对于任意可列的两两互不相容事件 $A_1, A_2, \dots, A_n, \dots$(即 $A_i \cap A_j = ∅$, $i \neq j$, $i, j = 1, 2, \dots$),有:
$$
P\left( \bigcup_{i=1}^{\infty} A_i \right) = \sum_{i=1}^{\infty} P(A_i),
$$
则称 $P(\cdot)$ 为概率,$P(A)$ 为事件 $A$ 的概率。
古典概型和几何概型
古典概型
条件:
- 只有有限个样本点(基本事件);
- 每个样本点(基本事件)发生的可能性都一样。
如果古典概型的基本事件总数为n,事件A包含k个基本事件,也叫作有利于A的基本事件为k个则A的概率为
$$
P(A)=\frac{k}{n}=\frac{\text{事件A所含基本事件的个数}}{\text{基本事件总数}}
$$
题目:
- 随机分配
- 简单随机抽样(先后有放回,先后无放回,任取)
几何概型
条件:
- 样本空间(基本事件空间)$\Omega$是一个可度量的有界区域;
- 每个样本点(基本事件)发生的可能性都一样,即样本点落入$\Omega$的某一可度量的子区域S的可能性大小与S的几何度量成正比,而与S的位置及形状无关。
在几何概型随机试验中,如果$S_A$是样本空间$\Omega$的一个可度量的子区域,则事件A={样本点落入区域$S_A$}的概率为
$$
P(A)=\frac{S_A\text{的几何度量}}{\Omega的几何度量}
$$
区别
古典概型与几何概型的区别:基本事件有限、等可能发生的随机试验为古典概型;基本事件无限且具有几何度量、等可能发生的随机试验为几何概型。
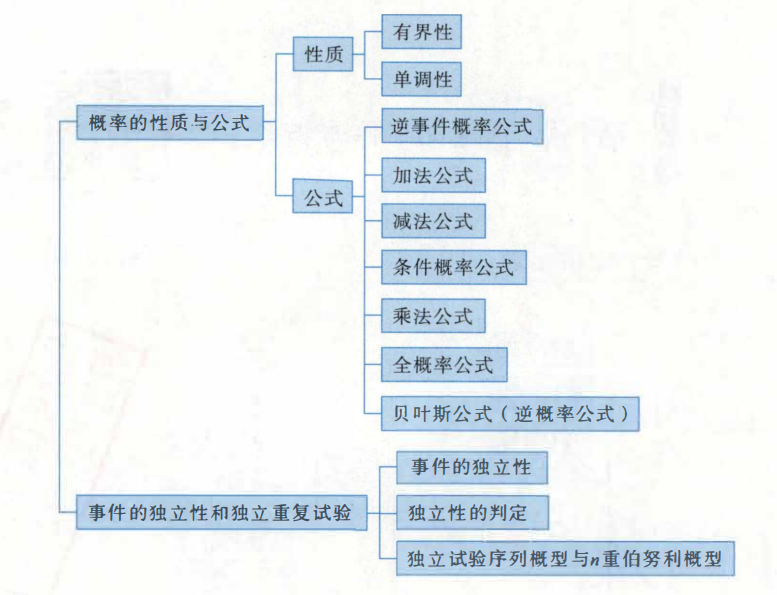
概率的性质与公式
性质
有界性:对于任一事件A,有0≤P(A)≤1,且P(∅)=0,P(2)=1
P(A)=0,不能断言A=∅;P(A)=1,不能断言A=$\Omega$.
单调性:$P(B-A)=P(B)-P(A),P(B)\geq P(A)$
公式
- $P(A)+P(\bar{A})=1$
- $P(A\cup B)=P(A)+P(B)-P(A\cap B)$
$P(A\cup B\cup C)=P(A)+P(B)+P(C)-P(A\cap B)-P(A\cap C)$
$-P(B\cap C)+P(A\cap B\cap C)$ - $P(A-B)=P(A)-P(AB)=P(A\bar{B})$
- 条件概率公式:$P(B|A)=\frac{P(AB)}{P(A)}$
- 乘法公式:如果$P(A)>0$,则$P(AB)=P(A)P(B|A)$
- 全概率公式 一个事件发生的概率=其他事件的条件下发生该事件的概率之和
- 贝叶斯公式
$$P(A_j|B)=\frac{P(A_j)P(B|A_j)}{\sum_{i=1}^{n}P(A_i)P(B|A_i)}(j=1,2,…,n)$$
tips:P(A ∪ B) = 1 不能推出 A ∪ B = 全集,且 P(A ∩ B) = P(A ∪ B) - P(A) - P(B) = 0 不能推出 A ∩ B = ∅
事件的独立性和独立重复试验
事件的独立性
P(AB)=P(A)P(B)
独立性的判定
- $A$与$B$相互独立=$A$与$\bar{B}$相互独立=$\bar{A}$与$B$相互独立=$\bar{A}$与$\bar{B}$相互独立
- 对独立事件组不含相同事件作运算,得到的新事件组仍独立,如A,B,C,D相互独立,则 AB与CD相互独立,A与BC-D相互独立.
- 若P(A)=0或P(A)=1,则A与任意事件B相互独立
两两独立:当一组随机事件中任意两个事件是独立的时
相互独立:一组事件中,任意子集的事件组合都是独立的
独立试验序列概型与n重伯努利概型
独立试验序列概型:
独立试验序列概型指的是一系列相互独立的试验,每个试验可能有不同的结果,且各个试验之间没有相互影响。独立性意味着每个试验的结果不依赖于其他试验的结果。
- 试验可以有两种或多种不同的结果。
- 各个试验之间是相互独立的,也就是说一个试验的结果不会影响其他试验的结果。
- 适用于描述多个相互独立的随机事件。
n重伯努利概型:
- 每次试验只有A与$\bar{A}$两个结果;
- 每次试验A发生的概率p=P(A)不变:
- 试验独立重复进行n次.
在n重伯努利概型中,事件A发生k次(只管次数,不论位置)的概率为$C_n^kp^k(1-p)^{n-k}(k=0,1,…,n)$,且如果用X表示n重伯努利概型中事件A发生的次数,则X服从二项分布B(n,p).